In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. Bernoulli's principle is named after the Dutch-Swiss mathematician Daniel Bernoulli who published his principle in his book Hydrodynamica in 1738.
Bernoulli's principle can be applied to various types of fluid flow, resulting in what is loosely denoted as Bernoulli's equation. In fact, there are different forms of the Bernoulli equation for different types of flow. The simple form of Bernoulli's principle is valid for incompressible flows (e.g. most liquid flows) and also for compressible flows (e.g. gases) moving at low Mach numbers. More advanced forms may in some cases be applied to compressible flows at higher Mach numbers.
Bernoulli's principle can be derived from the principle of conservation of energy. This states that in a steady flow the sum of all forms of mechanical energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy and potential energy remain constant. If the fluid is flowing out of a reservoir the sum of all forms of energy is the same on all streamlines because in a reservoir the energy per unit mass (the sum of pressure and gravitational potential ρ g h) is the same everywhere.
Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline, where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.
APPLICATIONS OF BERNOULLI’s PRINCIPLE
1. The carburetor used in many reciprocating engines contains a venturi to create a region of low pressure to draw fuel into the carburetor and mix it thoroughly with the incoming air. The low pressure in the throat of a venturi can be explained by Bernoulli's principle; in the narrow throat, the air is moving at its fastest speed and therefore it is at its lowest pressure.
A carburetor is a device that blends air and fuel for an internal combustion engine. It was invented by Karl Benz before 1885 and patented in 1886. It is colloquially called a carb. The word carburetor comes from the French carbure meaning "carbide". Carburer means to combine with carbon. In fuel chemistry, the term has the more specific meaning of increasing the carbon (and therefore energy) content of a fuel by mixing it with a volatile hydrocarbon.
2. The Pitot tube and static port on an aircraft are used to determine the airspeed of the aircraft. These two devices are connected to the airspeed indicator which determines the dynamic pressure of the airflow past the aircraft. Dynamic pressure is the difference between stagnation pressure and static pressure. Bernoulli's principle is used to calibrate the airspeed indicator so that it displays the indicated airspeed appropriate to the dynamic pressure.
A pitot tube is a pressure measurement instrument used to measure fluid flow velocity. The pitot tube was invented by the French engineer Henri Pitot in the early 1700s and was modified to its modern form in the mid 1800s by French scientist Henry Darcy. It is widely used to determine the airspeed of an aircraft and to measure air and gas velocities in industrial applications.
The basic pitot tube consists of a tube pointing directly into the fluid flow. As this tube contains fluid, a pressure can be measured; the moving fluid is brought to rest (stagnates) as there is no outlet to allow flow to continue. This pressure is the stagnation pressure of the fluid, also known as the total pressure or (particularly in aviation) the pitot pressure.
The measured stagnation pressure cannot of itself be used to determine the fluid velocity (airspeed in aviation). However, Bernoulli's equation states:
Stagnation Pressure = Static Pressure + Dynamic Pressure
Which can also be written
Solving that for velocity we get:
Where V is fluid velocity
and pt is stagnation or total pressure
and ps is static pressure
and ρ is fluid density
The dynamic pressure, then, is the difference between the stagnation pressure and the static pressure. The static pressure is generally measured using the static ports on the side of the fuselage. The dynamic pressure is then determined using a diaphragm inside an enclosed container. If the air on one side of the diaphragm is at the static pressure, and the other at the stagnation pressure, then the deflection of the diaphragm is proportional to the dynamic pressure, which can then be used to determine the indicated airspeed of the aircraft. The diaphragm arrangement is typically contained within the airspeed indicator, which converts the dynamic pressure to an airspeed reading by means of mechanical levers.
Instead of static ports, a pitot-static tube may be employed, which has a second tube coaxial with the pitot tube with holes on the sides, outside the direct airflow, to measure the static pressure.
Pitot tubes on aircraft commonly have heating elements called pitot heat to prevent the tube from becoming clogged with ice. The failure of these systems can have catastrophic consequences, as in the case of Austral Líneas Aéreas Flight 2553, Birgenair Flight 301 (investigators suspected that some kind of insect could have created a nest inside the pitot tube. The prime suspect is a species called the Black and yellow mud dauber wasp), Northwest Orient Airlines Flight 6231, AeroPeru Flight 603 (blocked static port), and of one X-31.


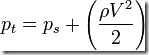



No comments:
Post a Comment